2025, A Year of Conferences -- Sandor Dargo
 Conferences are never just about the talks — they’re about time, travel, tradeoffs, and the people you meet along the way. After a year of attending several C++ events across formats and cities, this post is a personal look at how different conferences balance technical depth, community, and the experience of being there.
Conferences are never just about the talks — they’re about time, travel, tradeoffs, and the people you meet along the way. After a year of attending several C++ events across formats and cities, this post is a personal look at how different conferences balance technical depth, community, and the experience of being there.
2025, A Year of Conferences
by Sandor Dargo
From the article:
This year I had the chance to attend three conferences onsite, plus one online, and even a meetup in my hometown, Budapest. Depending on who you ask, maybe it’s not a lot — I know some speakers do twice as many. But if you ask my family, you’d probably get a different (and understandable) answer. For me — for us — it’s a lot. It’s also an honour and a privilege in many ways.
To express my appreciation and gratitude toward the organizers and the community, I do two things:
- I try to prepare well for my talks.
- I post trip reports soon after each event — usually within a week.
Those trip reports are moderately personal: I share which talks I liked and also some of my impressions, but I try to make them useful rather than purely personal. Still, I think that once in a while, a more personal, less serious post has its place — and that’s what this one wanted to be originally.
At one of the social dinners at CppCon, a developer working for a FAANG company in New York asked me which conference I’d recommend. My answer: it depends on your goals — and your budget and constraints.

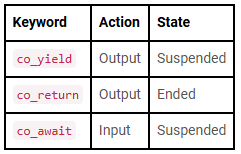 C++20 introduced coroutines. Quasar Chunawala, our guest editor for this edition, gives an overview.
C++20 introduced coroutines. Quasar Chunawala, our guest editor for this edition, gives an overview. Filtering items from a container is a common situation. Bartłomiej Filipek demonstrates various approaches from different versions of C++.
Filtering items from a container is a common situation. Bartłomiej Filipek demonstrates various approaches from different versions of C++. std::chrono::high_resolution_clock sounds like the obvious choice when you care about precision, but its name hides some important caveats. In this article, we’ll demystify what “high resolution” really means in <chrono>, why this clock is often just an alias, and when—if ever—it’s actually the right tool to use.
std::chrono::high_resolution_clock sounds like the obvious choice when you care about precision, but its name hides some important caveats. In this article, we’ll demystify what “high resolution” really means in <chrono>, why this clock is often just an alias, and when—if ever—it’s actually the right tool to use.